Project: Step 2.2
Haunted Target

Disclaimer: the automatically generated English translation is provided only for convenience and it may contain wording flaws. The original French document must be taken as reference!

Goals: Program a small automaton (which will take the form of a little ghost :)) chasing a target.

The `ChasingAutomaton` class

This section focuses on simulating how a simple automaton pursues a target present in its vicinity. The coded mechanisms will be used to implement target pursuit by animals (which will notably allow scorpions to eat lizards :-/).

This automaton will be implemented by a class ChasingAutomaton coded in the directory src/Animal.

In this project, we will consider that any simulated entity is potentially subject to encountering other entities. It can therefore be viewed abstractly as a Collider.

A ChasingAutomaton does not escape the rule. It is therefore a Collider characterized additionally by:

a direction of movement (of Vec2d);
the magnitude (norm) of its velocity (a double);
the position of the target it is pursuing (a Vec2d)
You will note that the ChasingAutomaton only foreshadows the notion of an Animal. It is therefore not integrated into the environment and has its own target (not integrated into the environment).

The ChasingAutomaton will also be characterized by data such as:

its maximum movement speed (a double);
its mass (still a double).

We want the values assigned to this data to be loadable on demand, from simulation configuration files (without having to recompile the program or reinitialize objects). Also, we will access them through these methods:

getStandardMaxSpeed() will return the constant CHASING_AUTOMATON_MAX_SPEED (maximum speed of the automaton);
getMass() will return the constant CHASING_AUTOMATON_MASS (automaton mass).

Another solution would have been to introduce these parameters as attributes. However, this leads to less convenient solutions if one wants to change the simulation parameters while it is running (we will have the opportunity to revisit this in later stages).

The constants used are defined in the file Utility/Constants.hpp

Finally, you will associate the following methods with ChasingAutomaton:

a setter setTargetPosition allowing to modify the target position (this will notably allow us to test how the automaton reacts to changes in the target's position);
a method getSpeedVector calculating the speed vector of the automaton (as the product of the direction with the speed norm);
a method void update(sf::Time dt) calculating the position and speed of the automaton after the time step dt has elapsed (see the graphics tutorial). This method will allow the automaton to move. The algorithm it implements is described below.
a method void draw(sf::RenderTarget& targetWindow) that draws the automaton and its target in the graphic window targetWindow. The target will be drawn like the one in the environment.
To graphically represent the automaton, you will use the small ghost image provided in the directory res/. Drawing an image can be done using the utility function buildSprite provided in the file Utility/Utility.[hpp][cpp]. You will proceed as follows:
```
        sf::Texture& texture = getAppTexture();
        auto image_to_draw(buildSprite(,
                                       ,
                                       texture));
        target.draw(image_to_draw);
    
```
The method getAppTexture() can be used after including Application.hpp; To avoid unnecessary circular dependencies between classes, make sure to include Application.hpp only in the file using this method. For example, if it is ChasingAutomaton.cpp that uses getAppTexture(), you must include Application.hpp in ChasingAutomaton.cpp and not in ChasingAutomaton.hpp (always apply the rule "include only what is necessary, where it is necessary"!).
- is the name of the file in the folder res/ containing the image to be used. As a file name, you will use the predefined constant GHOST_TEXTURE (provided in the file Utility/Constants.hpp).
- and are the position and size to assign to the image. For size, you can take the radius of the automaton as a Collider multiplied by two.
a constructor initializing the position using a value passed as a parameter and the radius to the constant CHASING_AUTOMATON_RADIUS (provided in Utility/Constants.hpp). The speed norm will have zero as the default value. The target position and direction will be initialized using vec2d (0,0) and (1,0) respectively.

You can currently leave the method update with an empty body.

Test 3: display of `ChasingAutomaton`

To test your developments, a graphical application is provided in Tests/GraphicalTests/ChasingTest.[hpp][cpp].

As in the previous test, the ChasingTest class inherits from the Application class. It has a specific attribute ChasingAutomaton. These are the methods you just programmed that are invoked in the test.

More precisely, the class ChasingTest redefines:

the onEvent method so that it draws the target of its ChasingAutomaton attribute when the user presses the 'T' key;
the method onDraw so that your method ChasingAutomaton::draw is invoked;
the method onUpdate which will invoke your method ChasingAutomaton::update (currently idle!).

The provided CMakeLists.txt file allows you to launch the test compilation through the chasingTest target. Don't forget to uncomment this target in the CMakeLists.txt file (lines 96, 97 and lines 139, 140) and execute Build >Run Cmake when you are ready to compile/test.

Running the graphics test should now allow you to display something like:

The target appears at (0,0) (top left corner): you can change its position values by positioning the mouse and clicking the 'T' key (as done in the screenshot above).

Alright... it's not very spectacular yet, the ghost doesn't seem very motivated by its target. It's time to start fixing that.

Time step movement algorithm dt: method `update`

In this project, we will start from a simple model where movement is governed by a system of differential equations of the type: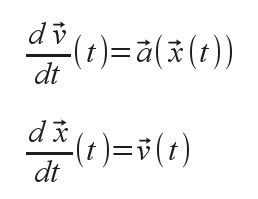

where x⃗(t) is the position of the automaton at time t, v⃗(t) its velocity and a⃗(x⃗(t)) the acceleration due to the application of the different forces to which the automaton may be subjected when it is at position x⃗(t).

A numerical method for solving such a system (called "Euler-Cromer method") consists of calculating the new velocity and new position as follows:

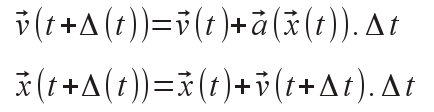
The acceleration will be modeled by a force whose calculation will be done specifically according to different situations: for example, for our ChasingAutomaton, the force will be an attractive force exerted by the target.

Specifically, the algorithm that will implement the update method of the ChasingAutomaton will be as follows:

calculation of the attraction force f exerted by the target;
acceleration = f / mass ;
new_speed = current_speed + acceleration * dt
nouvelle_direction = normalized new_speed
the new speed must be capped at the maximum speed of the automaton (if the norm of nouvelle_vitesse is greater than the maximum speed, nouvelle_vitesse is reduced to nouvelle_direction * vitesse maximale);
new_position = current_position + new_speed * dt

The update method thus calculates the new position and velocity of the automaton after the passage of a time step dt, when it is subjected to a force f. Do not forget to update the attributes of the ChasingAutomaton after these calculations.

For the sake of simplicity, it is not required to code the movement in the toroidal world (the methods of Vec2d are sufficient).

The ChasingAutomaton is expected to later become a more evolved "animal." The latter will no longer necessarily be governed in its movements by a force strictly linked to a target (the force will exist but will be calculated differently in certain situations). However, the update of position and speed from steps 2 to 6 will always be done in the same way. It is recommended to modularize these processes by creating two distinct methods: one responsible for the calculation of the force related to the attraction exerted by a target and the other related to the update of movement data (position, speed, and direction).

[Question Q2.5] What prototype do you propose for the two distinct suggested methods?

Explain and justify your choices in your REPONSES file.

Calculation of the force of attraction

The attractive force exerted by a target can be calculated as the vector: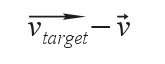

where v⃗ is the current speed of the automaton, and v⃗_target is the speed it wishes to have towards the target. The latter can be calculated as follows:

with :

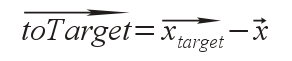
x⃗_target is the position of the target, x⃗ that of the automaton and maxSpeed the maximum speed of the latter.

The force of attraction is thus proportional to the distance between the automaton and the target.

deceleration is a constant used to modulate the deceleration towards the target. This constant ensures that the closer the automaton is to the target, the slower it moves. The goal is to avoid overshooting it (out of excessive zeal!).

[Question Q2.6] How would you propose to use an enumerated type to make the deceleration optionally equal to either: 0.9 (strong deceleration/low speed), 0.6 (medium deceleration and speed) or 0.3 (weak deceleration/high speed)? And how do you propose to integrate this choice element in your code if we want it to be dictated from the outside (so that we can decide on demand which deceleration we want to use depending on the situation)?

Explain and justify your choices in your file REPONSES.

Coding instructions for this section:

For a quick reminder on enumerated types, review the material from the first video of week 8 of last semester's MOOC: https://www.coursera.org/learn/initiation-programmation-cpp/lecture/aqXqY/puissance-4-introduction
if the distance between the automaton and the target is zero, the attractive force will also be zero;
you will ensure to properly modularize your processes;
time will be managed in seconds (dt.asSeconds, see the graphics tutorial)

Test 4: moving the `ChasingAutomaton`

To test the movement method you just programmed, you will proceed exactly the same way as for the previous graphical test.

At the end of this step, you should achieve the following behavior (shown here slightly sped up):

	← The user places the target using the mouse: the automaton must follow it and stop there (restart the video if needed).
[Video: Automaton pursuing a target]

Feel free to "play" with the maximum speed value in the constants file (and possibly the decelerations in your code) to see how the value choices affect the movement.

Back to project statement (part 2) Next module (part 2.3)

Project: Step 2.2 Haunted Target

Disclaimer: the automatically generated English translation is provided only for convenience and it may contain wording flaws. The original French document must be taken as reference!

The ChasingAutomaton class

Test 3: display of ChasingAutomaton