Projet : étape 2.2
Cible hantée

Buts: Programmer un petit automate (qui prendra la forme d'un petit fantôme :)) pourchassant une cible.

La classe `ChasingAutomaton`

Cette partie s'intéresse à simuler le fait qu'un automate simple poursuive une cible présente dans son voisinage. Les mécanismes codés seront utilisés pour mettre en place la poursuite d'une cible par les animaux (ce qui permettra notamment aux scorpions de manger des lézards :-/).

Cet automate sera mis en oeuvre par une classe ChasingAutomaton codée dans le répertoire src/Animal.

Dans ce projet, nous considérerons que toute entité simulée est potentiellement sujette à rencontrer d'autres entités. Elle peut donc être vue de façon abstraite comme un Collider.

Un ChasingAutomaton n'échappe pas à la règle. Il est donc un Collider caractérisé en plus par :

une direction de déplacement (des Vec2d);
la magnitude (norme) de sa vitesse (un double);
la position de la cible qu'il poursuit (un Vec2d)
Vous noterez que le ChasingAutomaton ne fait que préfigurer la notion d'Animal. Il n'est donc pas intégré à l'environnement et dispose d'une cible propre (non intégrée à l'environnement).

Le ChasingAutomaton sera également caractérisé par des données telles que:

sa vitesse maximale de déplacement (un double);
sa masse (encore un double).

Nous souhaitons que les valeurs attribuées à ces données puissent être chargées à la demande, depuis des fichiers de paramétrage de la simulation (et plus tard, sans avoir à recompiler le programme ou réinitialiser des objets). Aussi, nous allons y accéder via ces méthodes :

getStandardMaxSpeed() retournera la constante CHASING_AUTOMATON_MAX_SPEED (vitesse maximale de l'automate);
getMass() retournera la constante CHASING_AUTOMATON_MASS (masse de l'automate).

Une autre solution aurait consisté à introduire ces paramètres sous la forme d'attributs. Cela donne lieu cependant à des solutions moins confortables si l'on veut changer les paramètres de la simulation pendant que celle-ci s'exécute (nous aurons l'occasion d'y revenir dans les étapes ultérieures).

Les constantes utilisées sont définies dans le fichier Utility/Constants.hpp

Vous associerez enfin, les méthodes suivantes au ChasingAutomaton :

un setter setTargetPosition permettant de modifier la position de la cible (ceci nous permettra notamment de tester comment l'automate réagit à des changements de place de la cible);
une méthode getSpeedVector calculant le vecteur vitesse de l'automate (comme étant le produit de la direction avec la norme de la vitesse);
une méthode void update(sf::Time dt) calculant la position et la vitesse de l'automate au bout de l'écoulement du pas de temps dt (voir le tutoriel graphique). Cette méthode permettra à l'automate de se déplacer. L'algorithme qu'elle met en oeuvre est décrit ci-dessous.
une méthode void draw(sf::RenderTarget& targetWindow) qui dessine l'automate et sa cible dans la fenêtre graphique targetWindow. La cible sera dessinée comme celle de l'environnement.
Pour représenter graphiquement l'automate, vous utiliserez la petite image de fantôme fournie dans la répertoire res/. Le dessin d'une image peut se faire au moyen de la fonction utilitaire buildSprite fournie dans le fichier Utility/Utility.[hpp][cpp]. Vous procéderez comme suit:
```
        sf::Texture& texture = getAppTexture(<nom_fichier_image>);
        auto image_to_draw(buildSprite(<position_voulue>,
                                       <taille_voulue>,
                                       texture));
        target.draw(image_to_draw);
    
```
La méthode getAppTexture() est utilisable après inclusion de Application.hpp; Pour éviter les situations de dépendances circulaires inutiles entre classes, prenez soin de n'inclure Application.hpp que dans le fichier utilisant cette méthodee. Par exemple, si c'est ChasingAutomaton.cpp qui utilise getAppTexture(), il faut inclure Application.hpp dans ChasingAutomaton.cpp et non pas dans ChasingAutomaton.hpp (on applique toujours la règle «n'inclure que ce qui est nécessaire, à l'endroit où c'est nécessaire» !).
- <nom_fichier_image> est le nom du fichier du dossier res/ contenant l'image à utiliser. En guise de nom de fichier vous utiliserez la constante prédéfinie GHOST_TEXTURE (donnée dans le fichier Utility/Constants.hpp).
- <position_voulue> et <taille_voulue> sont la position et la taille à donner à l'image. Comme taille vous pourrez prendre le rayon de l'automate en tant que Collider multiplié par deux.
un constructeur initialisant la position au moyen d'une valeur passée en paramètre et le rayon à la constante CHASING_AUTOMATON_RADIUS (fournie dans Utility/Constants.hpp). La norme de la vitesse aura zéro comme valeur par défaut. La position de la cible et la direction seront initialisées au moyen des vec2d (0,0) et (1,0) respectivement.

Vous pouvez pour le moment mettre un corps vide à la méthode update.

Test 3 : affichage du `ChasingAutomaton`

Pour tester vos développements, une application graphique est fournie dans Tests/GraphicalTests/ChasingTest.[hpp][cpp].

Comme pour le test précédent, la classe ChasingTest hérite de la classe Application. Elle a comme attribut spécifique un ChasingAutomaton. Ce sont les méthodes que vous venez de programmer qui sont invoquées dans le test.

Plus précisément, la classe ChasingTest redéfinit:

la méthode onEvent de sorte à ce qu'elle affecte une position à la cible de son attribut ChasingAutomaton quand l'utilisateur appuie sur la touche 'T';
la méthode onDraw de sorte à ce que votre méthode ChasingAutomaton::draw soit invoquée;
la méthode onUpdate qui va invoquer votre méthode ChasingAutomaton::update (au chômage technique pour le moment !).

Le fichier CMakeLists.txt fourni permet de lancer la compilation du test par le biais de la cible chasingTest. N'oubliez pas de décommenter cette cible dans le fichier CMakeLists.txt (lignes 96, 97 et les lignes 139, 140) et d'exécuter Build >Run Cmake lorsque vous êtes prêt à compiler/tester.

L'exécution du test graphique devrait pour l'heure vous permettre d'afficher quelque chose comme :

La cible apparaît en (0,0) (tout en haut à gauche): vous pouvez modifier les valeurs de sa position en positionnant la souris et en cliquant sur la touche 'T' (ce qui a été fait dans la copie d'écran ci-dessus).

D'accord ... ce n'est pas encore très spectaculaire, le fantôme n'a pas l'air très motivé par sa cible. Il est temps de commencer à y remédier.

Algorithme de déplacement sur un pas de temps dt : méthode `update`

Dans ce projet, nous partirons d'un modèle simple où le déplacement est régi par un système d'équations différentielles de type :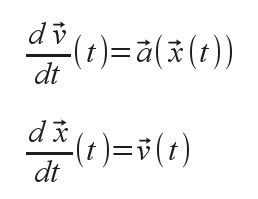

où x⃗(t) est la position de l'automate au temps t, v⃗(t) sa vitesse et a⃗(x⃗(t)) l'accélération dûe à l'application des différentes forces auxquelles l'automate peut être soumis lorsqu'il est à la position x⃗(t).

Une méthode numérique de résolution d'un tel système (appelée «méthode d'Euler-Cromer») consiste à calculer la nouvelle vitesse et nouvelle position comme suit :

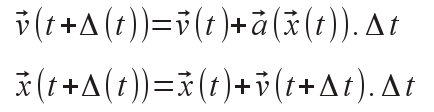
L'accélération sera modélisée par une force dont le calcul se fera spécifiquement en fonction de différentes situations: par exemple, pour notre ChasingAutomaton, la force sera une force d'attraction exercée par la cible.

Concrètement, l'algorithme que mettra en oeuvre la méthode update du ChasingAutomaton sera le suivant :

calcul de la force d'attraction f exercée par la cible;
acceleration = f / masse ;
nouvelle_vitesse = vitesse_courante + acceleration * dt
nouvelle_direction = nouvelle_vitesse normalisée
la nouvelle vitesse doit être plafonnée à la vitesse maximale de l'automate (si la norme de nouvelle_vitesse est supérieure à la vitesse maximale, nouvelle_vitesse se ramène à nouvelle_direction * vitesse maximale);
nouvelle_position = position_courante + nouvelle_vitesse * dt

La méthode update calcule donc ainsi la nouvelle position et vitesse de l'automate après l'écoulement d'un pas de temps dt, lorsqu'il est soumis à une force f. Ne pas oublier de mettre à jour les attributs du ChasingAutomaton après ces calculs.

Par souci de simplification, il n'est pas demandé de coder le déplacement dans le monde torique (les méthodes de Vec2d suffisent).

Le ChasingAutomaton est appelé à devenir plus tard un «animal» plus évolué. Ce dernier ne sera plus forcément régi dans ses déplacements par une force strictement liée à une cible (la force existera mais se calculera différemment dans certaines situations). Par contre, la mise à jour des position et vitesse des étapes 2 à 6 sera toujours faite de la même manière. Il est recommandé de modulariser ces traitements en créant deux méthodes distinctes: l'une en charge du calcul de la force liée à l'attraction exercée par une cible et l'autre liée à la mise à jour des données de déplacement (position, vitesse et direction).

[Question Q2.5] Quel prototype proposez-vous pour les deux méthodes distinctes suggérées ?

Explicitez et justifiez vos choix dans votre fichier REPONSES.

Calcul de la force d'attraction

La force d'attraction exercée par une cible peut-être calculée comme étant le vecteur :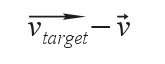

où v⃗ est la vitesse courante de l'automate, et v⃗_target la vitesse qu'il souhaite avoir vers la cible. Cette dernière peut se calculer comme suit :

avec :

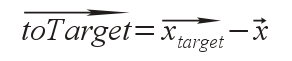
x⃗_target est la position de la cible, x⃗ celle de l'automate et maxSpeed la vitesse maximale de ce dernier.

La force d'attraction est ainsi proportionnelle à la distance séparant l'automate de la cible.

deceleration est une constante permettant de moduler la décélération vers la cible. Cette constante permet de faire en sorte que plus l'automate est proche de la cible, plus il est lent. Le but pour lui étant de ne pas la dépasser (par excès de zèle!).

[Question Q2.6] Comment proposeriez-vous d'utiliser un type énuméré pour faire en sorte que la décélération puisse valoir à choix : 0.9 (forte décélération/faible vitesse), 0.6 (décélération et vitesse moyennes) ou 0.3 (décélération faible/vitesse forte) ? Et comment proposez-vous d'intégrer cet élément de choix dans votre code si l'on souhaite qu'il soit dicté par l'extérieur (de sorte à pouvoir décider à la demande quelle décélération l'on veut utiliser selon la situation) ?

Explicitez et justifiez vos choix dans votre fichier REPONSES.

Indications pour le codage de cette partie :

Pour un petit rappel sur les types énumérés, revoir le matériel de la première vidéo de la semaine 8 du MOOC du semestre passé : https://www.coursera.org/learn/initiation-programmation-cpp/lecture/aqXqY/puissance-4-introduction
si la distance séparant l'automate de la cible est nulle, la force d'attraction sera aussi nulle;
vous veillerez à bien modulariser vos traitements;
le temps sera géré en secondes (dt.asSeconds, voir le tutoriel graphique)

Test 4 : déplacement du `ChasingAutomaton`

Pour tester la méthode de déplacement que vous venez de programmer, vous procéderez exactement de la même manière que pour le test graphique précédent.

Vous devriez, au terme de cette étape, obtenir le comportement suivant (montré ici un peu en accéléré) :

	← L'utilisateur place la cible au moyen de la souris : l'automate doit la suivre et s'y arrêter (redémarrez la vidéo au besoin) .
[Video : Automate poursuivant une cible]

N'hésitez pas à «jouer» avec la valeur de la vitesse maximale dans le fichier de constantes (et éventuellement les décélérations dans votre code) pour voir comment les choix de valeurs se répercutent sur le déplacement.

Retour à l'énoncé du projet (partie 2) Module suivant (partie 2.3)

Projet : étape 2.2 Cible hantée

La classe ChasingAutomaton

Test 3 : affichage du ChasingAutomaton