Projet : étape 2.3
Déambulations

La classe Animal

Nous disposons via la classe ChasingAutomaton d'une version rudimentaire d'« animal » capable de se diriger vers une cible. Il s'agit maintenant d'en faire un Animal et de sophistiquer un peu son comportement.

Concrètement, un Animal va avoir un comportement très voisin d'un ChasingAutomaton, à la différence près  :

1. qu'il ne poursuit une cible que si cette dernière est dans son champ de vision;
2. et qu'en l'absence de cible visible, il se promène de façon aléatoire dans son environnement.

Vous pouvez donc pour commencer, reprendre dans Animal l'intégralité des méthodes et attributs de la classe ChasingAutomaton en prenant garde de modifier les noms de constructeurs et destructeurs.

Champ de vision

1. l'angle θ (en radians) caractérisant son champ de vision (un double);
2. la distance maximale à laquelle il peut voir (un double).

Comme pour certaines des caractéristiques du ChasingAutomaton, nous allons faire en sorte que ces caractéristiques soient restituées par des méthodes :

• getViewRange() qui retournera la constante ANIMAL_VIEW_RANGE (angle de vision);
• getViewDistance() qui retournera la constante ANIMAL_VIEW_DISTANCE (distance maximale pour le champ de vision).

Le constructeur de Animal sera bien sûr mis à jour pour initialiser le rayon de l'animal à ANIMAL_RADIUS.

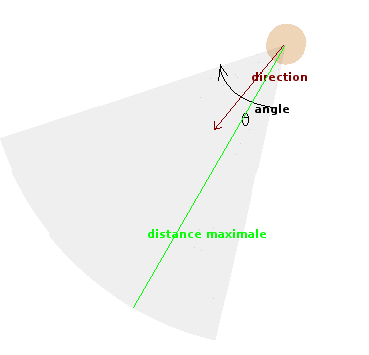
Vous doterez votre classe animal des méthodes suivantes relatives au vecteur direction  :

• getRotation retournant l'angle du vecteur direction en coordonnées polaires (méthode angle de vec2d);
• setRotation(angle) mettant à jour le vecteur direction pour une rotation de angle de l'animal (le vecteur direction vaudra simplement {cos(angle), sin(angle)}).

[Question Q2.7] Pourquoi selon vous est-il préférable de déclarer la méthode setRotation (et par le même raisonnement une éventuelle méthode setPosition de Collider) comme protégée  ?

Répondez à cette question dans votre fichier fichier REPONSES et adaptez votre code en conséquence (lorsque vous modifiez une classe déjà codée, n'oubliez pas de relancer les tests la concernant pour vérifier que l'ensemble du code reste fonctionnel).

Pour permettre de vérifier que la mise en oeuvre du déplacement de l'animal est correcte, il sera utile de pouvoir afficher concrètement son champ de vision.

Faites donc en sorte que la méthode draw de Animal, invoque une méthode drawVision affichant le champ de vision.

L'affichage du champs de vision d'un Animal devrait alors ressembler à la partie grisée ci-dessous :

Une méthode buildArc est fournie dans Utility/Utility.[hpp/cpp]. Pour afficher un arc de cercle entre 45° et 135°, en gris transparent, centré en mOrigin, de rayon mRadiusArc, vous écrirez:

    sf::Color color = sf::Color::Black;
    color.a = 16; // light, transparent grey
    Arc arc(buildArc(45,135, mRadiusArc, mOrigin, color));
    targetWindow.draw(arc);
    

Test 5 : affichage du champ de vision

Le fichier de test Tests/GraphicalTests/AnimalTest est fourni pour tester ces derniers développements. Il fonctionne selon des principes analogues à ceux des tests graphiques précédents : AnimalTest hérite de la classe Application .

Par héritage AnimalTest dispose donc d'un attribut de type Environment. La méthode Application::getAppEnv donne accès à cet attribut.

La classe AnimalTest redéfinit la méthode onEvent de sorte à ce que la touche 'T' correponde à appel de la méthode addTarget qui va ajouter une cible à l'environnement à l'endroit où est positionnée la souris. La méthode onSimulationStart de la classe AnimalTest, quant à elle, crée un animal et l'ajoute à la faune du même environnement.

La classe méthode run héritée de Application invoque en boucle le dessin de l'environnement.

[Question Q2.8] Que devez-vous modifier pour que le dessin de l'environnement tienne compte de la présence de l'animal (et donc l'affiche aussi) ?

Répondez à cette question dans votre fichier fichier REPONSES.

Le fichier CMakeLists.txt fourni permet de lancer la compilation du test par le biais de la cible animalTest. N'oubliez pas de décommenter cette cible dans le fichier CMakeLists.txt (lignes 104, 105 et les lignes 146, 147) et d'exécuter Build >Run Cmake lorsque vous êtes prêt à compiler/tester.

Vous devriez voir se produire l'affichage suivant :

Perception d'une cible

Notre Animal a désormais un champ de vision. Il nous faut encore programmer le fait qu'il ne perçoit effectivement que ce qui y est !

Une méthode isTargetInSight prenant en argument la position d'une cible et testant si l'animal la perçoit, compte tenu de son champ de vision, semble donc s'imposer. Cette méthode retournera true si l'Animal «voit» la cible et false sinon.

Soit d⃗ le vecteur x⃗_cible - x⃗, où x⃗_cible est la position de la cible et x⃗ celle de l'animal, les conditions à remplir pour que ce dernier perçoive la cible sont les suivantes:

1. la cible soit suffisamment proche: |d⃗| <= distMax
   la méthode sqrt utilisée par la méthode Vec2d::length est coûteuse. Il est préférable d'utiliser Vec2d::lengthSquared.
2. la cible soit dans l'angle de vision : o⃗ .d⃗_n >= cos(Θ/2) (voir ce lien), où d⃗_n est le vecteur distance (entre this et la cible) normalisé, o⃗ le vecteur direction de this, et Θ, l'angle de vision. Pour que l'angle soit pris inclusivement, il faut lui ajouter un petit "offset" : Θ + 0.001 par exemple.
   Si |d⃗| vaut zéro, la méthode isTargetInSight devra retourner true. Pour éviter les erreurs de précision des représentations en virgule flottante, vous utiliserez la méthode isEqual fournie dans Utility/Utility.[hpp][cpp])

Test 6 : perception d'une cible

Le fichier de test Tests/UnitTests/TargetInSightTest est fourni pour tester ces derniers développements. Il s'agit cette fois d'un test unitaire non graphique (à l'image de ceux utilisés lors de l'étape précédente pour tester la classe Collider).

[Question Q2.9] (avancée) Pour pouvoir tester différentes configurations (cibles dans le champ de vision et hors de celui-ci), il est nécessaire ici de pouvoir faire varier à volonté le vecteur direction de l'animal. Pour se donner cette liberté, le test TargetInSightTest redéfinit une sous-classe de Animal appelée DummyAnimal (juste utilisée pour les besoins du test). Sauriez-vous expliquer pourquoi ? Répondez à cette question, si vous le souhaitez, dans votre fichier REPONSES.

Pour pouvoir lancer ce test, décommenter la cible targetInSightTest dans le fichier CMakeLists.txt (toujours aux deux endroits).

Vous devriez alors obtenir une trace d'exécution ressemblant à ceci  :

===============================================================================
All tests passed (9 assertions in 1 test case)

Cibles de l'environnement : adaptation de Animal::update

La méthode update, qui met à jour le déplacement de Animal au cours du temps, est pour l'instant identique à celle mise en place pour le ChasingAutomaton :

1. elle calcule la force exercée par la cible de l'automate;
2. elle met à jour le déplacement compte tenu de cette force.
   Une orientation/direction nulle n'a pas vraiment de sens pour les animaux. On ne mettra donc à jour la direction que si la nouvelle valeur calculée est non nulle. Sinon, l'animal gardera son ancienne direction.

Le ChasingAutomaton avait connaissance de la cible à atteindre sans que cette dernière ne fasse partie d'un environnement. Les cibles visibles par un Animal lui seront par contre transmises par l'environnement.

Il faut donc adapter la méthode update, dans cet esprit :

1. chercher les cibles de l'environnement vues par l'animal;
2. en choisir une;
3. s'il y en a au moins une, la stocker comme cible de l'animal;
1. calculer la force exercée par cette cible
2. mettre à jour le déplacement compte tenu de cette force

Commencez donc par programmer la méthode Environment::getTargetsInSightForAnimal qui prend en argument un pointeur sur un Animal et qui retourne l'ensemble des cibles de l'environnement qu'il voit.

[Question Q2.10] Quel type de retour proposez-vous pour cette méthode ? Répondez à cette question dans votre fichier REPONSES.

Apportez ensuite les modifications nécessaires à la méthode Animal::update.

class Animal;

Test 7  : l'animal se déplace vers une cible de l'environnement

Le fichier de test Tests/GraphicalTests/AnimalTest permet de continuer à tester vos développements.

La classe AnimalTest dispose d'une méthode update héritée de Application. Cette méthode invoque la mise à jour de l'environnement après l'écoulement d'un pas de temps.

[Question Q2.11] Que devez-vous modifier pour que la mise à jour de l'environnement tienne compte de la présence de l'animal (et donc invoque les mises-à-jour nécessaires sur les animaux au bout de l'écoulement d'un pas de temps dt) ? Répondez à cette question dans votre fichier fichier REPONSES.

Vous pourrez relancer le test AnimalTest au moyewn de la cible animalTest.

Promenades au hasard

Pour l'heure, la méthode update fait en sorte que l'animal se déplace vers une cible de l'environnement. Quand il n'y a aucune cible visible il reste donc immobile.

Il s'agit maintenant d'implémenter la dernière fonctionnalité importante de cette étape: celle permettant à l'Animal de se déplacer au hasard si aucune cible n'est visible.

Cibles virtuelles

Pour implémenter cette fonctionnalité nous allons en fait reprendre le même principe que celui de la poursuite d'une cible. La cible sera simplement ici virtuelle : un simple point généré "au hasard" à une certaine distance de l'animal.

Concrètement, l'idée est de générer un point au hasard sur un cercle à une certaine distance de l'animal (la cible est le point bleu dans l'image ci-dessous). Ce point deviendra la nouvelle cible de l'animal (ici simplement représenté par le cercle en rose) :

Au terme de cette étape, l'algorithme Animal::update devra donc être mis à jour comme suit :

1. chercher les cibles de l'environnement vues par l'animal;
2. en choisir une;
3. s'il y en a au moins une, calculer la force exercée par cette cible et la stocker dans f;
4. sinon:
   1. générer une cible virtuelle;
   2. calculer la force d'attraction exercée par cette cible et la stocker dans f : ce sera simplement la différence x⃗_cible - x⃗, où x⃗_cible est la position de la cible virtuelle et x⃗ celle de l'animal (voir image ci-dessous).
5. mettre à jour le déplacement (position et vitesse) compte tenu de f.

Le calcul de la force d'attraction exercée par la cible virtuelle utilise les vecteurs positions exprimées dans le repère global :

Il vous est demandé maintenant de programmer la méthode randomWalk qui met en oeuvre les étapes 4.1 et 4.2 de l'algorithme de Animal::update

Méthode randomWalk()

Cette méthode utilisera trois nouvelles caractéristiques de l'animal, restituées par des méthodes, pour générer la cible virtuelle :

1. le rayon du cercle sur lequel sera générée la cible virtuelle (méthode getRandomWalkRadius() retournant la constante ANIMAL_RANDOM_WALK_RADIUS);
2. la distance du centre de ce cercle à la position de l'animal (méthode getRandomWalkDistance() retournant la constante ANIMAL_RANDOM_WALK_DISTANCE);
3. et un facteur d'amplification du déplacement de la cible virtuelle (méthode getRandomWalkJitter() retournant la constante ANIMAL_RANDOM_WALK_JITTER).

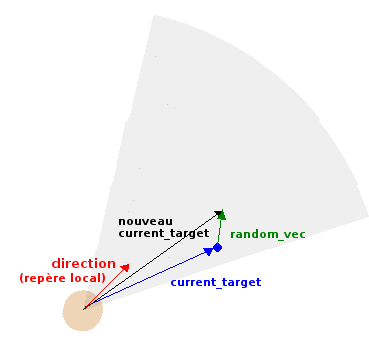
Soit current_target la cible virtuelle poursuivie par l'animal lors d'un cycle de simulation (qui sera exprimée dans son repère local)

Pour calculer la valeur de current_target à l'étape suivante il faudra  :

1. générer un Vec2d random_vec dont chacun des composants est tiré aléatoirement entre -1.0 et 1.0;
   La méthode uniform définie dans le fichier fourni Random/Random.hpp permet de générer des nombres aléatoires uniformément distribués. L'appel uniform(-1.0,1.0) devrait répondre à vos besoins ici.
2. calculer current_target += random_vec * getRandomWalkJitter() (voir étape 2 de la figure ci-dessous);
3. normaliser current_target et multipliez le par getRandomWalkRadius (current_target se trouve alors sur un cercle de rayon ANIMAL_RANDOM_WALK_RADIUS (voir étape 3 de la Figure ci-dessous);
4. calculer la position de current_target sur le cercle déplacé de getRandomWalkDistance() : Vec2d moved_current_target = current_target + Vec2d(getRandomWalkDistance(), 0) (voir étape 4 de la Figure ci-dessous);

Soit x⃗_cible la conversion de moved_current_target dans le repère global. La force régissant le mouvement est donc simplement x⃗_cible - x⃗, où x⃗ est la position de l'animal.

étape 2	étape 3	étape 4

Comme nous l'avons vu précédemment, le calcul de la force d'attraction exercée par la cible virtuelle nécessite de connaître ses coordonnées dans le repère global. Il faut donc procéder à une conversion.

Conversion en coordonnées globales

Écrivez une méthode ConvertToGlobalCoord convertissant un Vec2d exprimé dans le repère local d'un Animal, en un Vec2d dans le repère global.

La librairie SFML fournit l'outillage nécessaire au travers de la notion de matrices de transformation. Soit local un Vec2d exprimé dans le repère local d'un Animal. Pour le convertir dans le repère global, il suffit de lui faire subir une translation à la position de l'animal et une rotation de γ, où γ est l'angle du vecteur direction de l'animal . En utilisant les matrices de transformation cela se fait comme suit :

        // create a transformation matrix
       sf::Transform matTransform;

       // first, translate
       matTransform.translate(position_animal); 

       // then rotate
       matTransform.rotate(γ);

       // now transform the point
       Vec2d global = matTransform.transformPoint(local);
       

La translation amène le système de coordonnées au niveau de la position de l'animal, la rotation permet de l'aligner sur la direction de l'animal. On obtient ainsi le repère local de l'animal. La dernière instruction permet de calculer la coordonnée globale du point exprimé dans ce repère local.

Test 8 : déplacement des animaux finalisé

Vous pourrez relancer le test AnimalTest comme précédemment:

Votre programme devrait alors avoir un comportement analogue à celui montré par la petite vidéo ci-dessous :

Déplacez la souris et appuyez sur la touche 'T' pour créer une cible dans l'environnement. Le seul Animal de l'environnement doit déambuler au hasard et quand la cible entre dans on champ de vision, il doit s'y diriger. Pour que le test soit correct, il faut que le déplacement dans un monde torique soit correctement visualisable et qu'appuyer sur la touche 'R' efface les cibles. Notez qu'à ce stade l'animal se dessine en principe toujours chez vous comme un fantôme et la cible virtuelle (bille bleue sur le cercle jaune) n'est pas encore affichée. Quelques indications sont données plus bas pour y remédier.

[Video : déplacement aléatoire d'un animal avec champ de vision et cible]

Test 9 : dessin de la cible virtuelle

Pour faciliter la vérification de votre algorithme de déplacement aléatoire, il est utile de faire afficher la cible virtuelle suivie par l'animal en l'absence de cible réelle.

Ajoutez cette facilité à votre programme que devrait alors afficher la cible virtuelle sous le format suivant :

Enfin (facultatif à cette étape), si vous trouvez votre l'aspect de votre "animal" trop .. "vintage video game", vous pouvez lui associer la texture donnée par la constante ANIMAL_TEXTURE.

Afin qu'il soit orienté proprement (c'est à dire que son champs de vision soit plutôt devant lui), vous pouvez utiliser le dernier argument de la fonction buildSprite. Cet argument permet de faire subir à l'image une rotation d'un angle donné.

Votre programme devrait alors avoir le comportement montré par la petite vidéo ci-dessous :