Choisissez votre style : colorisé, impression

Série 15 :
Remise en jambe

Buts

Cette série a pour but de vous faire réviser les notions vues au semestre passé.

Préliminaires :

Si vous avez installé QTCreator et SFML au dernier semestre, vous pouvez travailler sur votre propre machine (il suffit d'ouvrir le fichier CMakeLists.txt lorsque fourni). Sinon, cette série est à réaliser sur les VMs de l'EPFL car tous les outils et la librairie graphique nécessaires y sont installés, Vous pouvez donc soit directement vous logguer sur une des machines des salles de TP soit vous y connecter à distance depuis un ordinateur personnel.

Rappels importants du premier semestre :

Connexion à distance depuis une machine personnelle : pour vous connecter à distance sur une VM de l'EPFL, procédez comme au point 2. sous "Travail de l'environnement de l'EPFL" de l'exercice "Mise en place de l'environnement de travail" du cours ICC.
Stockage nécessaire dans le dossier Desktop/myfiles : sur les VMs de l'EPFL il faut impérativement stocker vos fichiers/dossiers dans le dossier Desktop/myfiles (ou éventuellement posixfs) si vous voulez les conserver d'une session à l'autre.

Avant d'effectuer les manipulations décrites dans cette série, créez le répertoire ~/Desktop/myfiles/Programmation/cpp/serie15 (i.e. créez le sous-répertoire serie15 dans le répertoire ~/Desktop/myfiles/Programmation/cpp).

Enfin, n'oubliez pas de vous inscrire au MOOC : https://www.coursera.org/learn/programmation-orientee-objet-cpp dont vous devrez commencer à étudier le matériel pour le cours de la semaine prochaine.

Exercice 1 : Courbes de von Koch (remise en jambe, niveau 1 et 2)

Nous allons dans cet exercice faire une petite incursion dans l'univers des fractales et écrire une fonction permettant de dessiner ce que l'on appelle des "courbes de Von Koch" (voir ce lien) :

Préliminaires :

Il s'agit donc ici de compléter un petit programme graphique que vous lancerez au moyen d'outils permettant la compilation séparée (compilation d'un programme constitué de plusieurs fichiers). Nous aborderons plus en détail le thème de la compilation séparée dans deux semaines. La bibliothèque graphique utilisée est la SFML (c'est celle que vous utiliserez durant votre projet).

Commencez par procéder aux manipulations suivantes :

copiez l'archie fournie vonkoch-sfml.zip dans un répertoire serie15/vonkoch

Dézippez cette archive : unzip vonkoch-sfml.zip :

cd
cd Desktop/myfiles/Programmation/cpp/serie15/vonkoch
unzip vonkoch-sfml.zip
rm vonkoch-sfml.zip

Lancez le programme QTCreator, et ouvrez y le fichier fourni dans ce répertoire et nommé CMakeLists.txt. Procédez comme indiqué ici https://iccsv.epfl.ch/series-prog/install/installation-tutorial.php#qtcreator-cmakeproject depuis la section "Création du projet".
Lancez le programme avec la petite flèche verte sur le bandeau latéral gauche en choisissant la cible mandelbrot.

l'ensemble de Mandelbrot

Alternativement, vous pouvez aussi lancer le programme en ligne de commande dans un terminal avec les comnandes suivantes tapées telles qu'elles (attention les points sont importants) :

 cmake .
 make mandelbrot
 ./mandelbrot

Ouvrez maintenant le fichier fourni src/vonkoch1.cc. Vous y trouverez notamment la fonction drawLine permettant de dessiner une droite entre les points de coordonnées (x1,y1) et (x2,y2).

Il vous est demandé de programmer dans ce fichier, la fonction void ligne_brisee((sf::RenderTarget& target, double x1, double y1, double x2, double y2)

qui trace la ligne brisée représentée par la figure ci_dessous :

avec :

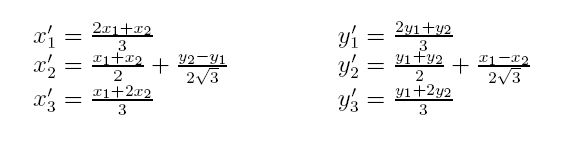
Pour tester votre fonction de tracé de ligne brisée, vous pouvez maintenant lancer a cible vonkoch1 dans QTCreator.

Alternativement , vous pouvez vous placer dans le répertoire cpp/serie15 et tapez les commandes :

make clean
make  vonkoch1
./vonkoch1

Vous deviez voir se produire l'affichage suivant :

Notez que les constantes utilisées dans le programme principal viennent du fichier fourni Config.h (qui est inclu en début de programme).

Lorsque tout marche bien, ouvrez alors le fichier src/vonkoch2.cc et copiez-y votre fonction ligne_brisee.

Ecrivez ensuite une fonction récursive von_koch(sf::RenderTarget& target, int depth, double x1, double y1, double x2, double y2) qui:

Si depth (profondeur) vaut zéro, trace la ligne brisée telle que précédemment,
Sinon, se rappelle quatre fois sur les quatre segments constituant la ligne brisée, mais avec une profondeur depth-1.

La figure ci-dessous, illustre ce que produit cette fonction avec depth valant 1 (profondeur de 1):

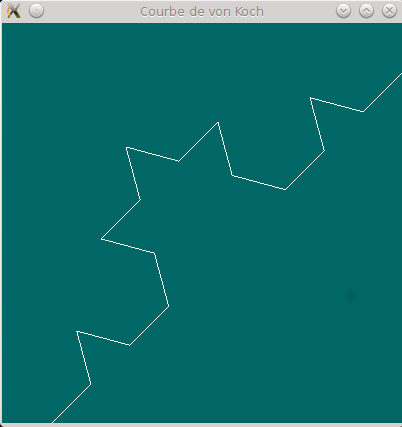
Lancez le programme complété au moyen de la cible vonkoch2 dans QTCreator ou des commandes suivantes dans le terminal :

make clean
make vonkoch2
./vonkoch2

L'idée est de ne produire le dessin à proprement parler (la ligne brisée) qu'une fois que l'on aura atteint le niveau de profondeur zéro.

Si l'on appelle la fonction von_koch avec le niveau de profondeur 2 par exemple, il y aura 4 appels à la fonction sur chacun des segments s1, s2, s3 et s4 (avec la profondeur 1) qui à leur tour entraîneront chacun 4 nouveaux appels sur chacun des 16 sous-segments constituant s1, s2, s3 et s4 (avec cette fois le niveau 0). La ligne brisée sera alors dessinée sur chacun des 16 sous-segments ce qui donnera ceci :

Dans le programme principal fourni, commentez la ligne affichant une courbe de von Koch unique et décommentez la partie du programme affichant quatre courbes reliées entre elles. Relancez le programme au moyen des commandes ci-dessus.

Vous devriez voir apparaître le "flocon" suivant :

Vous pouvez ensuite changer la profondeur en modifiant la constante DEPTH dans le fichier fourni Config.h et relancer le programme. Vous verrez alors plusieurs variantes du flocon.

Exercice 2 : codes de Huffman (structures, tableaux, fonctions, ..., niveau 2 et 3)

Cet exercice peut être réalisé avec l'éditeur de votre choix (Geany ou QtCreator autre).

Mise en place

copiez l'archive fournie huffman.zip dans un répertoire serie15/huffman

Dézippez cette archive : unzip huffman.zip :

cd
cd Desktop/myfiles/Programmation/cpp/serie15/huffman
unzip huffman.zip
rm huffman.zip

Lancez le programme QTCreator, et ouvrez y le fichier fourni dans ce répertoite et nommé CMakeLists.txt. Procédez comme indiqué ici https://iccsv.epfl.ch/series-prog/install/installation-tutorial.php#qtcreator-cmakeproject depuis la section "Création du projet".
Lancez le programme avec la petite flèche verte sur le bandeau latéral gauche en choisissant la cible huffman.

Tâche

Le but de cet exercice est de réaliser des codes de Huffman de textes (cf cours ICC: https://drive.switch.ch/index.php/s/Ljua6p0eo9nVOH). Le principe du code de Huffman (binaire) est assez simple : il consiste à regrouper les deux « entités » les moins probables à chaque étape; une « entité » étant soit une lettre de départ, soit un groupe d'entités déjà traitées (une, deux, trois, ... lettres déjà traitées).

Le plus simple est peut être de commencer directement par l'algorithme lui-même à un niveau d'abstraction assez haut (approche descendante) :
à partir de la distribution de probabilité initiale des lettres (leur compte), on va, de proche en proche tant qu'il nous reste plus que deux « entités » à traiter

rechercher les deux entités les moins probables ;
ajouter le symbole '0' devant tous les codes déjà produits pour la première de ces deux entités ;
ajouter le symbole '1' devant tous les codes déjà produits pour la seconde de ces deux entités ;
fusionner ces deux entités en une nouvelle entité, dont on calcule la probabilité : somme des probabilités des deux entités fusionnées;
pour cela on écrasera une de ces deux entités par leur fusion et on supprimera l'autre.

Notez qu'on a donc une entité de moins à chaque fois (la fusion supprime les deux entités, mais n'en rajoute qu'une seule nouvelle).

Il nous faut donc représenter ces « entités » (et un ensemble d'entités). Nous vous proposons de le faire de la façon suivante :

une « entités » est simplement un groupe de lettres avec sa probabilité ;
le groupe de lettres peut simplement être représenté par la liste des positions de ces lettres (voir ci-dessous) ;
au départ, ces entités correspondent simplement aux lettres du mot avec leur probabilité.

Nous aurons aussi besoin de représenter le code lui-même. Un code est une bijection entre les mots à coder et leur code. La bonne structure de données pour représenter cela est ce que l'on appelle des « tables associatives », que nous n'avons pas encore vues (fin du semestre). A ce stade du cours, nous vous proposons donc simplement de représenter le code comme un tableau dynamique de structures contenant:

le mot à coder (type « chaîne de caractères ») ; dans les exemple du cours, c'est simplement une seule lettre, mais on pourrait généraliser ;
la probabilité correspondante ;
le mode de code correspondant (type « chaîne de caractères »)).

Prenons un exemple : supposons que l'on veuille coder la phrase « JE PARS A PARIS ».

On commencera par créer un « code » (il n'est pas complet à ce stade, tous ses mots sont vides) contenant par exemple (ordre de lecture ici, mais vous pouvez changer cet ordre, bien sûr):

"J", probabilité : 1./15., mot de code vide;
"E", probabilité : 1./15., ...(mot de code vide);
" ", probabilité : 3./15., ...;
"P", probabilité : 2./15., ...;
"A", probabilité : 3./15., ...;
etc.
"I", probabilité : 1./15., mot de code vide.

Une fois ce « code » (mots vides) créé, on pourra créer la version initiale de la liste d'« entités » nécessaires pour l'algorithme décrit plus haut (ordonnée à nouveau ici dans l'ordre de lecture, mais vous pouvez choisir un autre ordre):

indices : 0, probabilité : 1./15.;
cette entité représente la lettre "J", lettre à la position 0 dans le « code » (mots vides) précédemment créé ;
indices: 1, probabilité : 1./15.;
indices: 2, probabilité : 2./15.;
etc.
indices: 7, probabilité : 1./15..

Pour l'instant cette liste d'« entités » ne semble pas très intéressante et semble faire double emploi avec le code : c'est normal : le code de Huffman commence par les lettres seules.

Mais dès la première étape de codage, cela va changer : on commence par regrouper les deux moins probables, disons par exemple le "J" et le "E" (les deux premiers moins probables dans l'ordre de lecture, là encore votre choix peut être différent suivant comment vous écrivez l'algorithme, cela ne change rien au final sur la longueur moyenne du code). On aura alors une nouvelle entité :
indices: 0, 1, probabilité : 2./15.;
et la liste d'« entités » devient (elle ne contient plus que 7 éléments):

indices: 0, 1, probabilité : 2./15.;
indices: 2, probabilité : 2./15.;
etc.
indices: 7, probabilité : 1./15..

Et comme dit au départ de cet exercice : une fois la fusion ci-dessus effectuée (ou même avant), on ajoutera respectivement '0' et '1' à chacun des mots de code correspondants. Dans cet exemple précis, cela à revient à les ajouter à chacun des deux mots de code, vides, de "J" et "E".

Voilà pour les structures de données proposées pour cet algorithme.

Pour l'algorithme lui-même : adoptez (bien sûr !) une démarche très modulaire en introduisant des fonctions pour chacune des tâches élémentaires ; par exemple : compter les lettres, normaliser les probabilités, fusionner 2 entités, rechercher les deux entités les moins probables, ajouter un symbole à un mot de code, construire les entités initiales à partir d'un « code » (mots vides), etc.

Vous trouverez ici un exemple de comment peut évoluer l'arbre (ensemble d'entités) et le code (ensemble de mots de code) pour l'exemple "JE PARS A PARIS" (avec tranche de 1).

Le but est de coder un programme bien modularisé qui pourra être testé au moyen du programme principal suivant :

 // ======================================================================
void test(string const& texte, size_t tranche)
{
  cout << "==== Par tranches de taille " << tranche << endl;
  Code c(calcule_probas(texte, tranche));
  //affiche_code(c);
  Huffman(c);
  affiche_code(c);
  string tc(encode(texte, c));
  cout << "taille orig. = " << texte.size() << " lettres/octets" << endl;
  cout << "taille codee = " << tc.size() << " bits = " << 1 + (tc.size() - 1) / 8 << " octets" << endl;
  cout << "long. moyenne  = " << double(tc.size()) /  double(texte.size()) << " bits" << endl; 
  cout << "compression  = " << 100.0 - 100.0 * tc.size() / (8.0 * texte.size()) << '%' << endl; 
  cout << "texte codé : " << tc << endl;
  cout << "check : " << decode(tc, c) << endl;
}
 
// ======================================================================
int main()
{
  string texte;
  
   // lecture d'un seul mot
  cout << "Entrez un mot : ";
  cin >> texte;
  test(texte, 1);

  // lecture d'une phrase complète
  cout << "Entrez une chaîne : " << flush;

  // on purge le flot d'entrée de tous les séparateurs
  // qui y sont restés
  cin >> ws;
  getline(cin, texte);
  test(texte, 2);
  
  texte = "Un petit texte a compresser : le but de cet exercice est de realiser des codes de Huffman de textes. Le principe du code de Huffman (binaire) est assez simple : il consiste a regrouper les deux mots les moins probables a chaque etape.";
 
  test(texte, 1);
  test(texte, 2);
  test(texte, 3);
  test(texte, 5);


  return 0;
}

Voici un exemple d'exécution possible:

Entrez un mot : spring
==== Par tranches de taille 1
"s" --> "100" (0.166667)
"p" --> "101" (0.166667)
"r" --> "111" (0.166667)
"i" --> "01" (0.166667)
"n" --> "00" (0.166667)
"g" --> "110" (0.166667)
taille orig. = 6 lettres/octets
taille codee = 16 bits = 2 octets
long. moyenne  = 2.66667 bits
compression  = 66.6667%
texte codé : 1001011110100110
check : spring
Entrez une chaîne : welcome back to programming
==== Par tranches de taille 2
"we" --> "0100" (0.0714286)
"lc" --> "0101" (0.0714286)
"om" --> "0111" (0.0714286)
"e " --> "1011" (0.0714286)
"ba" --> "1111" (0.0714286)
"ck" --> "001" (0.0714286)
" t" --> "1101" (0.0714286)
"o " --> "1001" (0.0714286)
"pr" --> "1000" (0.0714286)
"og" --> "1100" (0.0714286)
"ra" --> "000" (0.0714286)
"mm" --> "1110" (0.0714286)
"in" --> "1010" (0.0714286)
"g " --> "0110" (0.0714286)
taille orig. = 27 lettres/octets
taille codee = 54 bits = 7 octets
long. moyenne  = 2 bits
compression  = 75%
texte codé : 010001010111101111110011101100110001100000111010100110
check : welcome back to programming 
==== Par tranches de taille 1
"U" --> "01110100" (0.0042735)
"n" --> "01111" (0.0299145)
" " --> "00" (0.183761)
"p" --> "10100" (0.034188)
"e" --> "110" (0.166667)
"t" --> "0110" (0.0555556)
"i" --> "11111" (0.0470085)
"x" --> "101010" (0.017094)
"a" --> "0101" (0.0470085)
"c" --> "11100" (0.0384615)
"o" --> "10010" (0.034188)
"m" --> "111011" (0.025641)
"r" --> "0100" (0.0470085)
"s" --> "1011" (0.0769231)
":" --> "0111011" (0.00854701)
"l" --> "10001" (0.0299145)
"b" --> "100111" (0.017094)
"u" --> "10000" (0.0299145)
"d" --> "11110" (0.042735)
"H" --> "1010111" (0.00854701)
"f" --> "100110" (0.017094)
"." --> "1110101" (0.00854701)
"L" --> "01110101" (0.0042735)
"(" --> "0111001" (0.0042735)
")" --> "11101001" (0.0042735)
"z" --> "10101101" (0.0042735)
"g" --> "10101100" (0.0042735)
"h" --> "11101000" (0.0042735)
"q" --> "0111000" (0.0042735)
taille orig. = 234 lettres/octets
taille codee = 962 bits = 121 octets
long. moyenne  = 4.11111 bits
compression  = 48.6111%
texte codé : 0111010001111001010011001101111101100001101101010100110110000101001110010010111011101000
10011010111011110010000011101100100011100010011110000011000111101100011100110011000110101010110010011
10011111111001100011010110110001111011000010011001011000111111101111001000011110110101100111001001011
11011010110011110110001010111100001001101001101110110101011110011110110000110110101010011011010111110
10100011101011100010100010011111011111110011111101001100011110100000011100100101111011000111101100010
10111100001001101001101110110101011110001110011001111111101111010111111010011011101001001101011011000
01011011101111010101101001011111111110111010010001110000111011001111110001001110010010011111011111111
01101101100001010001001101010110001001001010000101001100100001000111010110011110110100001010100011101
11001001101011001000111010110011101110010111110111110110010100010010010100111010110011110001110101100
010100111001110100001010111000100001100011001100101101001101110101
check : Un petit texte a compresser : le but de cet exercice est de realiser des codes de Huffman de textes. Le principe du code de Huffman (binaire) est assez simple : il consiste a regrouper les deux mots les moins probables a chaque etape.
==== Par tranches de taille 2
"Un" --> "0110000" (0.00854701)
" p" --> "011001" (0.017094)
"et" --> "011011" (0.017094)
"it" --> "0110001" (0.00854701)
" t" --> "101111" (0.017094)
"ex" --> "00001" (0.025641)
"te" --> "00010" (0.025641)
" a" --> "00011" (0.025641)
" c" --> "00100" (0.025641)
"om" --> "0111111" (0.00854701)
"pr" --> "100111" (0.017094)
"es" --> "0100" (0.0598291)
"se" --> "100011" (0.017094)
"r " --> "1100111" (0.00854701)
": " --> "1010011" (0.00854701)
"le" --> "111001" (0.017094)
" b" --> "1010111" (0.00854701)
"ut" --> "1110111" (0.00854701)
" d" --> "0101" (0.0598291)
"e " --> "0011" (0.0512821)
"ce" --> "111101" (0.017094)
"t " --> "100001" (0.017094)
"er" --> "00101" (0.025641)
"ci" --> "100101" (0.017094)
" e" --> "1111111" (0.00854701)
"st" --> "1100011" (0.00854701)
"re" --> "011101" (0.017094)
"al" --> "1011011" (0.00854701)
"is" --> "110111" (0.017094)
"od" --> "1101011" (0.00854701)
"Hu" --> "110110" (0.017094)
"ff" --> "110100" (0.017094)
"ma" --> "011100" (0.017094)
"n " --> "101100" (0.017094)
"de" --> "110000" (0.017094)
"s." --> "000001" (0.00854701)
" L" --> "1001001" (0.00854701)
"in" --> "111100" (0.017094)
"pe" --> "1000001" (0.00854701)
"u " --> "1110100" (0.00854701)
"co" --> "111000" (0.017094)
"(b" --> "1110101" (0.00854701)
"ai" --> "1010101" (0.00854701)
") " --> "1000100" (0.00854701)
"as" --> "1000101" (0.00854701)
"z " --> "1001101" (0.00854701)
"si" --> "1100101" (0.00854701)
"mp" --> "0111100" (0.00854701)
" :" --> "0111101" (0.00854701)
" i" --> "0110101" (0.00854701)
"l " --> "0110100" (0.00854701)
"ns" --> "101110" (0.017094)
" r" --> "1100100" (0.00854701)
"eg" --> "1001100" (0.00854701)
"ro" --> "101000" (0.017094)
"up" --> "1010100" (0.00854701)
" l" --> "111110" (0.017094)
"eu" --> "1000000" (0.00854701)
"x " --> "1001000" (0.00854701)
"mo" --> "000000" (0.00854701)
"ts" --> "1101010" (0.00854701)
" m" --> "1011010" (0.00854701)
"oi" --> "1100010" (0.00854701)
"ba" --> "1111110" (0.00854701)
"bl" --> "1110110" (0.00854701)
"ha" --> "1010110" (0.00854701)
"qu" --> "1010010" (0.00854701)
"ap" --> "1100110" (0.00854701)
"e." --> "0111110" (0.00854701)
taille orig. = 234 lettres/octets
taille codee = 685 bits = 86 octets
long. moyenne  = 2.92735 bits
compression  = 63.4081%
texte codé : 0110000011001011011011000110111100001000100001100100011111110011101001000111100111101001111
10011010111111011101010011111101100001000010010110010111110111111111100011010100110111011011011110111001
01010101000010011010110100010100111101101101000111001011001100001011110000100010000001100100100111001111
11100100101100000101011110100111000110000010100111101101101000111001011001110101111100101010101110110001
00010010000110001011000111001101110010101111001110010111101011010101101001110001011101101110001000011110
01001001100101000101010000101111110010001011000000100100000000011010101111100100101101011000101011100110
01101000111111011101100100000110010010101101010010001101101111001100111110
check : Un petit texte a compresser : le but de cet exercice est de realiser des codes de Huffman de textes. Le principe du code de Huffman (binaire) est assez simple : il consiste a regrouper les deux mots les moins probables a chaque etape.
==== Par tranches de taille 3
"Un " --> "1100010" (0.0128205)
"pet" --> "1100011" (0.0128205)
"it " --> "1101001" (0.0128205)
"tex" --> "110111" (0.025641)
"te " --> "1101011" (0.0128205)
"a c" --> "01111" (0.025641)
"omp" --> "1111111" (0.0128205)
"res" --> "101111" (0.0128205)
"ser" --> "001111" (0.0128205)
" : " --> "000111" (0.0128205)
"le " --> "01011" (0.025641)
"but" --> "100111" (0.0128205)
" de" --> "11001" (0.0384615)
" ce" --> "1110111" (0.0128205)
"t e" --> "1110011" (0.0128205)
"xer" --> "100011" (0.0128205)
"cic" --> "000011" (0.0128205)
"e e" --> "001011" (0.0128205)
"st " --> "101011" (0.0128205)
"de " --> "111101" (0.025641)
"rea" --> "010010" (0.0128205)
"lis" --> "010011" (0.0128205)
"er " --> "010001" (0.0128205)
"des" --> "01100" (0.025641)
" co" --> "1111001" (0.0128205)
" Hu" --> "00100" (0.025641)
"ffm" --> "00000" (0.025641)
"an " --> "10000" (0.025641)
"tes" --> "101001" (0.0128205)
". L" --> "1110001" (0.0128205)
"e p" --> "1110101" (0.0128205)
"rin" --> "010101" (0.0128205)
"cip" --> "100101" (0.0128205)
"e d" --> "000101" (0.0128205)
"u c" --> "001101" (0.0128205)
"ode" --> "101101" (0.0128205)
"(bi" --> "011101" (0.0128205)
"nai" --> "1111101" (0.0128205)
"re)" --> "1101101" (0.0128205)
" es" --> "110000" (0.0128205)
"t a" --> "1101100" (0.0128205)
"sse" --> "1111100" (0.0128205)
"z s" --> "011100" (0.0128205)
"imp" --> "101100" (0.0128205)
": i" --> "001100" (0.0128205)
"l c" --> "000100" (0.0128205)
"ons" --> "100100" (0.0128205)
"ist" --> "010100" (0.0128205)
"e a" --> "1110100" (0.0128205)
" re" --> "1110000" (0.0128205)
"gro" --> "101000" (0.0128205)
"upe" --> "1111000" (0.0128205)
"r l" --> "010000" (0.0128205)
"es " --> "01101" (0.025641)
"deu" --> "101010" (0.0128205)
"x m" --> "001010" (0.0128205)
"ots" --> "000010" (0.0128205)
" le" --> "100010" (0.0128205)
"s m" --> "1110010" (0.0128205)
"oin" --> "1110110" (0.0128205)
"s p" --> "100110" (0.0128205)
"rob" --> "000110" (0.0128205)
"abl" --> "001110" (0.0128205)
"haq" --> "101110" (0.0128205)
"ue " --> "1111110" (0.0128205)
"eta" --> "1101010" (0.0128205)
"pe." --> "1101000" (0.0128205)
taille orig. = 234 lettres/octets
taille codee = 473 bits = 60 octets
long. moyenne  = 2.02137 bits
compression  = 74.7329%
texte codé : 11000101100011110100111011111010110111111111111011110011110001110101110011111001111011
111100111000110000110010111010111111010100100100110100010110011110010110011001001000000010000111101
110111101001111000111101010101011001010001010011011011011100100100000001000001110111111011101101110
000110110011111000111001011000101100110000010010010001010011101001110000101000111100001000001101101
010001010000010100010111001011101101001100001100011100110101111101110111111011010101101000
check : Un petit texte a compresser : le but de cet exercice est de realiser des codes de Huffman de textes. Le principe du code de Huffman (binaire) est assez simple : il consiste a regrouper les deux mots les moins probables a chaque etape.
==== Par tranches de taille 5
"Un pe" --> "100010" (0.0212766)
"tit t" --> "100011" (0.0212766)
"exte " --> "100101" (0.0212766)
"a com" --> "100111" (0.0212766)
"press" --> "101111" (0.0212766)
"er : " --> "111111" (0.0212766)
"le bu" --> "01111" (0.0212766)
"t de " --> "11011" (0.0425532)
"cet e" --> "00111" (0.0212766)
"xerci" --> "110011" (0.0212766)
"ce es" --> "00011" (0.0212766)
"reali" --> "01011" (0.0212766)
"ser d" --> "111011" (0.0212766)
"es co" --> "101011" (0.0212766)
"des d" --> "101001" (0.0212766)
"e Huf" --> "111001" (0.0212766)
"fman " --> "01001" (0.0212766)
"de te" --> "00001" (0.0212766)
"xtes." --> "110001" (0.0212766)
" Le p" --> "110101" (0.0212766)
"rinci" --> "00101" (0.0212766)
"pe du" --> "01101" (0.0212766)
" code" --> "111101" (0.0212766)
" de H" --> "101101" (0.0212766)
"uffma" --> "10000" (0.0212766)
"n (bi" --> "101100" (0.0212766)
"naire" --> "111100" (0.0212766)
") est" --> "01100" (0.0212766)
" asse" --> "00100" (0.0212766)
"z sim" --> "110100" (0.0212766)
"ple :" --> "110000" (0.0212766)
" il c" --> "00000" (0.0212766)
"onsis" --> "01000" (0.0212766)
"te a " --> "111000" (0.0212766)
"regro" --> "101000" (0.0212766)
"uper " --> "101010" (0.0212766)
"les d" --> "111010" (0.0212766)
"eux m" --> "01010" (0.0212766)
"ots l" --> "00010" (0.0212766)
"es mo" --> "110010" (0.0212766)
"ins p" --> "00110" (0.0212766)
"robab" --> "01110" (0.0212766)
"les a" --> "111110" (0.0212766)
" chaq" --> "101110" (0.0212766)
"ue et" --> "100110" (0.0212766)
"ape. " --> "100100" (0.0212766)
taille orig. = 234 lettres/octets
taille codee = 263 bits = 33 octets
long. moyenne  = 1.12393 bits
compression  = 85.9509%
texte codé : 10001010001110010110011110111111111101111110110011111001100011110110101111101110101
110100111100101001000011100011101010010101101111101101101100001011001111000110000100110100110000
000000100011100010100010101011101001010000101100100011001110111110101110100110100100
check : Un petit texte a compresser : le but de cet exercice est de realiser des codes de Huffman de textes.
Le principe du code de Huffman (binaire) est assez simple : il consiste a regrouper les deux mots les moins
probables a chaque etape.

Série 15 : Remise en jambe