Project: step 4.2
Scorpion with neural system
Disclaimer: the automatically generated English translation is provided only for convenience and it may contain wording flaws. The original French document must be taken as reference!
Goals: Simulate the internal mechanisms of predation in the scorpion
The objective of this step is to program the class NeuronalScorpion capable of simulating the predation mechanisms of the scorpion.
We will consider that NeuronalScorpion is equipped with 8 sensors located at the end of its legs. To simplify, these sensors will be equidistant from the center of the scorpion, on a radius getAppConfig().scorpion_sensor_radius from the Vec2d serving as the scorpion's position:
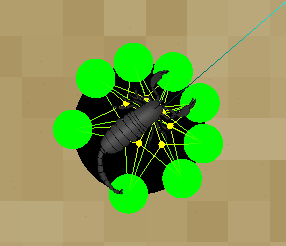 | ← simplified modeling of sensors (green circles) The CircularCollider has been drawn in black for better visibility. |
Start by creating an empty Sensor class.
Then code a primer of the class NeuronalScorpion derived from Scorpion . A NeuronalScorpion is characterized by:
- all of its 8 sensors, located at angles {18, 54, 90, 140, -140, -90, -54, -18} (in degrees) in the local reference frame of the animal;
- its estimation of the direction towards the target (which will be calculated using signals perceived by the sensors, a Vec2d);
We will see a little later that the NeuronalScorpion will be in different states (similar to the standard Scorpion ). When one of its sensors is activated, the scorpion goes into a state indicating that it perceives the signals of a wave and will remain in this state for a limited time. When this time is up, it will deactivate all of its sensors.
[Question Q4.5] How do you propose to represent all the sensors and their angles in NeuronalScorpion ? Answer this question in your file ANSWERS , justifying your choices.
The calculation made by NeuronalScorpion to estimate the direction of its target will depend on the position of its sensors. It is therefore wise to provide this class with a getPositionOfSensor method returning the position of a given sensor in the global reference frame.
[Question Q4.6] What prototype do you propose for the getPositionOfSensor method? Answer this question in your file ANSWERS , justifying your choices.
It is now a matter of modeling the sensors more precisely.
The sensors
Each sensor is essentially characterized by:
- a state (active or not);
- a score that quantifies its perception of a wave;
- a degree of inhibition , inhibitor , which results from the perception of inhibition signals emitted by other sensors, and which "temper" the score according to the formula score += 2.0 * (1.0 - inhibitor)
- The degree of inhibition is a value between 0 and getAppConfig().sensor_inhibition_max. You should ensure that the value of this attribute is capped at these values in case of modification.
- A sensor will be built with a score and a degree of inhibition of zero.
Activation and inhibition of sensors
A sensor is activated when the waves that touch it (or more precisely that touch its position) accumulate an intensity exceeding a certain threshold (getAppConfig().sensor_intensity_threshold).
The intensity of the waves in the environment at a given point is calculated as the sum of the intensities of each wave at that point.
The intensity of a wave at a point location is calculated as follows: if location is on the radius of the wave (to the nearest getAppConfig().wave_on_wave_marging ), and if location belongs to one of the arcs of the latter, then the intensity will be calculated as described here , otherwise it will be zero.
[Question Q4.7] What method(s) do you add and to which class(es) so that a sensor can know the cumulative intensity of the waves that touch it; without coding overly intrusive getters giving access to all the waves in the environment? Answer this question in your file file REPONSES and adapt your code accordingly.
As soon as it is activated, a sensor will increase its score with each simulation step. It will also begin to inhibit a number of sensors located in front of it.
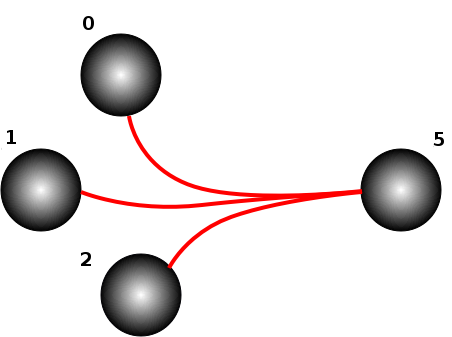 | ← the sensor 5 inhibits sensors 0, 1, and 2
|
Let s i be a sensor connected to the sensor this . Over a time step dt , this will act on s i by increasing its degree of inhibition proportionally to its own score (the higher the score of this , the more it inhibits s i ). Concretely, the degree of inhibition of s i will be increased by the score of this multiplied by getAppConfig().sensor_inhibition_factor .
To summarize, at each simulation step and as long as it is active, a sensor increases the degree of inhibition of the sensors connected to it and updates its own score by increasing it by 2.0 * (1.0 - inhibitor).
When inactive, the sensor will listen for potential waves. The algorithm is simply as follows: if the intensity of a wave perceived at the sensor's position is strong enough (greater than getAppConfig().sensor_intensity_threshold), the sensor becomes active.
[Question Q4.8] The sensor, to know its position, therefore needs to know the scorpion to which it belongs. What does this imply in terms of dependencies between the classes NeuronalScorpion and Sensor ? How do you manage it? Answer these questions in your file ANSWERS .
[Question Q4.9] Does this have an impact on how to build a sensor? Answer these questions in your file file REPONSES by justifying your answer.
Given the above, provide the complete coding for the Sensor class. This class should derive from Updatable and update its score and inhibition level according to the previous description. You won't worry about drawing the sensors for now .
As mentioned previously, the NeuronalScorpion is only sensitive to sensor activation for a limited time. Once this time has elapsed, it will deactivate all of its sensors.
Simulation of NeuronalScorpion
Now that the sensors are coded, we can complete the behavioral aspects of the NeuronalScorpion . The operation of this type of scorpion (method update and updateState ) only takes into account predation .
Below you will find information on:
- how the NeuronalScorpion estimates the direction towards a target;
- how to redefine its update and updateState methods.
Estimation of the direction towards a target
The direction towards the target estimated by the scorpion is simply the resultant:
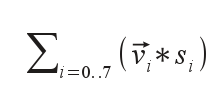
where s i is the score of sensor i and v⃗ i its position vector.
- clearly, v⃗ i will be worth
SCORPION_SENSOR_RADIUS * {cos(α i + θ), sin(α i + θ)}
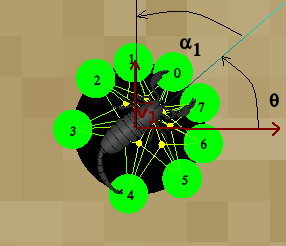
- the angles αi, associated with each sensor, have been described above;
- think about the Animal::getRotation() method!
Score of an estimate
An estimate d⃗ of the target direction will be associated with a score given simply by the norm of d⃗ .
States of the scorpion
The behavior of a NeuronalScorpion is conditioned by states different from those of the Scorpion (to take into account only predation in particular):
- IDLE: at rest (in this state it is receptive to waves possibly emitted by lizards);
- WANDERING : wandering randomly;
- TARGET_IN_SIGHT : a prey has entered its field of vision;
- MOVING: he does not yet see the prey but has perceived it through emitted waves (and then orients himself accordingly).
[Question Q4.10] How and where do you propose to model the possible states? Answer this question in your file file REPONSES by justifying your choices.
[Question Q4.11] How do you propose to model the clocks associated with states? Answer this question in your file file REPONSES justifying your choices.
Method update
The implemented algorithm is as follows:
- update of the sensors;
- if one of its sensors is active, manage the time during which the scorpion takes it into account (is receptive);
- If this time exceeds the maximum time getAppConfig().sensor_activation_duration , calculate d⃗ (the estimate of the direction to the target) and reset the sensors
- Updating its state (method updateState specialized compared to Scorpion ): see below;/li>
- calculation of the force f that manages the movement :
- in the WANDERING state: same calculation as for the standard scorpion;
- in the TARGET_IN_SIGHT state: same calculation as for the standard scorpion in the FOOD_IN_SIGHT state;
- in the MOVING state:
- manage the clock linked to this state;
- if estimating the direction toward the target involves rotating it more than scorpion_rotation_angle_precision , rotate it that much and calculate f as a slowing force toward the target (similar to what is suggested in here ); if you haven't programmed the slowing part, you can do the calculation as you did in the other analogous cases, e.g. FEEDING );
- otherwise (the angle is insufficient) move the scorpion straight ahead by a given step p (10 for example, but it is better to link the value of this step to the dimensions of the world). The force f is then a force of attraction towards a virtual target located at the position {p,0} of the scorpion's local frame;
- In the IDLE state: no force is exerted (the clock linked to this state must however be managed);
- update the movement (position, speed and direction) taking into account f.
Method updateState
- find the entities in the environment seen by the animal
- among this set of entities, choose the closest edible entity;
- if there is one, memorize it and switch to the TARGET_IN_SIGHT state;
- otherwise:
- if we are already in the IDLE state: evaluate the score related to the direction of a target . If it is sufficient (greater than getAppConfig().scorpion_minimal_score_for_action ) move to the MOVING state. Otherwise, if we have already been in the IDLE state for more than 5 seconds, we move to the WANDERING state;
- in the MOVING state: if you are in this state for more than 3 seconds you return to the IDLE state. The scorpion thus becomes receptive to new waves and forgets those already perceived previously (remember to update the direction of the target accordingly);
- in the WANDERING state: if one of the sensors has become active, we move to the IDLE state;
- in the TARGET_IN_SIGHT state: we move to the IDLE state (we are in the else of step 4 of the algorithm).
[Question Q4.12] What actions related to the management of the different clocks involved must you undertake and in which states of the scorpion? Answer this question in your file file REPONSES by justifying your answer.
Constructors
To be compatible with the provided test files, the NeuronalScorpion will have constructors with signatures similar to those coded for Scorpion . It will have WANDERING as its default state. The estimated direction of the target is of course zero initially.
Test 26: wave perception
The provided test NeuronalTest.cpp , which you can run using the command scons NeuronalTest-run for example, allows you to test the scorpion's perception of waves.
It is programmed so that a left click with the mouse creates a wave. You should see the scorpion orient itself based on the perception of this wave as shown by the following video:
| [Video: Neural model of the scorpion] |
Also test the fact that obstacles block the scorpion's perception of waves.
If the scorpion does not behave as desired, some graphical supplements can help you "debug" your code.
Test 27: Displays in "Debugging" mode
To verify your developments, complete the display in "debugging" mode so as to:
- show the scorpion's sensors;
- display its states ( MOVING , IDLE etc);
- adapt the color of the sensors according to their state, for example:
- in magenta if the sensor is active and has an inhibition degree greater than 0.2;
- in blue if it is inactive and has an inhibition degree greater than 0.2;
- in red if it has an inhibition degree less than 0.2 and is active
- in green otherwise
You should be able to observe a functioning similar to that shown in the short video below.
| [Video: Display of the neural model in "debugging" mode] |
The "debugging" mode display will allow you to verify that the obstacles indeed block the activation of the neurons.
| [Video: Obstacles preventing neuron activation] |
Test 28: waves and neurons
The provided test FinalApplication.cpp allows you to test the coexistence of a NeuronalScorpion and a WaveLizard in an environment.
The test launch modalities will be as follows:
- start by launching the test using the application target;
- then switch to "individual scale simulation" mode using the Tab key;
- put the simulation in pause mode using the space bar;
- create a NeuronalScorpion using the N key and a wave-emitting lizard using the W key;
- restart the simulation again using the space bar
The scorpion should then be able to locate the lizard using the waves it emits, as shown in the video below:
| [Video: Scorpion detecting a lizard outside its field of vision thanks to the perception of waves it emits while walking.] |
The neural model simulation is now complete. Congratulations on achieving the desired result! In the final stage of the project, you will refine the simulation tool a bit and have the opportunity to code some freely chosen extensions.
Back to project statement (part 4) Previous module (part 4.1)